NÚMEROS REALES
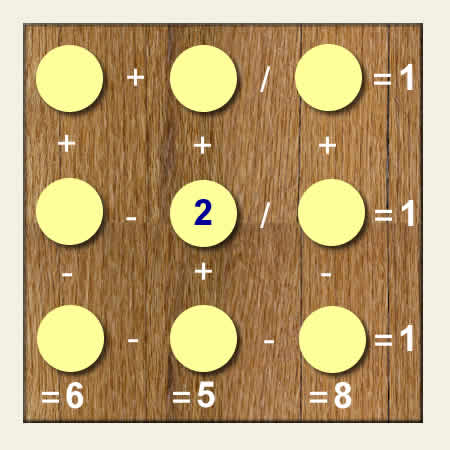
RETO MATEMÁTICO
Completar con los números del 1 al 9 que hagan verdadero el resultado
Los números
reales son el conjunto que incluye los números
naturales, enteros, racionales e irracionales. Se representa
con la letra ℜ.
Números naturales
De la necesidad de
contar objetos surgieron los números naturales. Estos son los números con los
que estamos más cómodos: 1, 2, 3, 4, 5, 6, ...hasta el infinito. El conjunto de
los números naturales se designa con la letra mayúscula N.
Todos los números están
representados por los diez símbolos : 0, 1, 2, 3, 4, 5, 6. 7, 8, y 9, que
reciben el nombre de dígitos.
Ejemplo
Los números naturales nos
sirven para decir cuántos compañeros tenemos en clases, la cantidad de flores
que hay en un ramo y el número de libros que hay en una biblioteca.
Números enteros
El conjunto de los números
enteros comprende los números naturales y sus números simétricos. Esto incluye
los enteros positivos, el cero y los enteros negativos. Los números negativos
se denotan con un signo "menos" (-). Se designa por la letra
mayúscula Z y se representa como:
Un número simétrico es aquel
que sumado con su correspondiente número natural da cero. Es decir, el
simétrico de n es -n, ya que:
Los enteros positivos son
números mayores que cero, mientras que los números menores que cero son los
enteros negativos.
Los números enteros nos
sirven para:
·
representar números
positivos: ganancias, grados sobre cero, distancias a la derecha;
·
representar números
negativos: deudas, pérdidas, grados bajo cero y distancias a la izquierda.
Ejemplos
En el polo Norte la
temperatura está por debajo de 0ºC durante casi todo el año, entre -43 ºC y
-15ºC en invierno. Una persona compra un vehículo por 10.000 pesos pero solo
tiene 3.000 pesos.
Esto significa que queda
debiendo 7.000 pesos.
Números racionales
Los números fraccionarios
surgen por la necesidad de medir cantidades continuas y las divisiones
inexactas. Medir magnitudes continuas tales como la longitud, el volumen y el
peso, llevó al hombre a introducir las fracciones. El conjunto de números
racionales se designa con la letra Q:
Ejemplos
Un pastel dividido entre tres
personas se representa como 1/3 un tercio para cada persona; una décima parte de
un metro es 1/10 m= 0,1m.
Números irracionales
Los números irracionales
comprenden los números que no pueden expresarse como la división de enteros en
el que el denominador es distinto de cero. Se representa por la letra
mayúscula I.
Aquellas magnitudes que no
pueden expresarse en forma entera o como fracción que son inconmensurables son
también irracionales. Por ejemplo, la relación de la circunferencia al diámetro
el número π=3,141592…
Las raíces que no pueden
expresarse exactamente por ningún número entero ni fraccionario, son números
irracionales:
Propiedades de los números reales
1.
La suma de dos
números reales es cerrada, es decir, si a y b ∈ ℜ, entonces a+b ∈ ℜ.
2.
La suma de dos
números reales es conmutativa, entonces a+b=b+a.
3.
La suma de números
es asociativa, es decir, (a+b)+c= a+(b+c).
4.
La suma de un número
real y cero es el mismo número; a+0=a.
5.
Para cada número
real existe otro número real simétrico, tal que su suma es igual a 0: a+(-a)=0
6.
La multiplicación de
dos números reales es cerrado: si a y b ∈ ℜ, entonces a . b ∈ ℜ.
7.
La multiplicación de
dos números es conmutativa, entonces a . b= b. a.
8.
El producto de
números reales es asociativo: (a.b).c= a.(b .c)
9.
En la multiplicación,
el elemento neutro es el 1: entonces, a . 1= a.
10.
Para cada número
real a diferente de cero, existe
otro número real llamado el inverso multiplicativo, tal que: a . a-1 =
1.
11.
Si a, b
y c ∈ ℜ, entonces a(b+c)= (a . b) + (a . c)

ACTIVIDAD
1.Completar la siguiente tabla con los símbolos e o e/
Numero
|
N
|
Z
|
Q
|
I
|
R
|
5
|
|||||
TI
|
|||||
-8
|
|||||
4
|
|||||
453
|
|||||
-1
|
|||||
3.5
|
|||||
2.23232323…
|
|||||
7,6
|
|||||
23
|
|||||
1
|
3. En el siguiente diagrama ubicar 2 ejemplos de cada conjunto numérico


Comentarios
Publicar un comentario